Formuliamo un problema abbastanza semplice, rilevare il Sarcasmo.

Diamo un’occhiata ad un paio di recensioni sarcastiche su prodotti venduti online. Intuitivamente, se una recensione ha un riscontro positivo ma un voto basso, allora “probabilmente” è sarcastica. Esempi:

Ero stanco di essere approcciato da bellissime ragazze. Dopo che ho comprato questa giacca, problema risolto. (Rating 0.5/5).

Ne ho acquistati due per sicurezza. Ho piacevolmente notato così che quando li accendo e li punto contro la parete posso varcare lo Star Gate. (Rating 0.5/5)

La semantica delle frasi ci suggerisce un sentiment positivo (“problema risolto”, “piacevolmente”), ma il rating è basso. Questo è un indizio di sarcasmo.

Ora che sospettiamo che c’è una qualche relazione tra il sentiment, il rating e il sarcasmo. Assegnamogli dei punteggi.

– Sentiment (+1 se positivio, 0 se neutro, -1 se negativo).
– Rating (da 0 a 5).
– Sarcasmo (1 per Si, 0 per No).

E tiriamo fuoti una lista di data points analizzando una certa quantità di recensioni.

(Sentiment, Rating, Sarcasm)
(1, 0.5, 1)
(1, 1, 1)
(1, 5, 0)
(-1, 4, 1)
(-1, 1, 0)
... e così via

Dunque per tirare fuori la relazione, dobbiamo lavorare sui valori di Rating e Sentiment, in modo da tirare fuori un valore per Sarcasm.
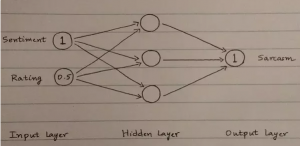
Useremo vari livelli (layer) per arrivare da un input ad un output. Diamo un’occhiata al primo esempio (1, 0.5, 1):

Rete neurale – esempio 1

Ogni linea nella rete ha un certo peso (weight). Useremo questi pesi per calcolare i valori nei cerchi del layer nascosto (hidden layer) e nel layer di output (il quale speriamo sia 1).
Inizialmente assegniamo dei pesi in maniera Randomica.

Rete neurale

In questo modo otteniamo la nostra prima rete neurale “stupida”. Vediamo quale sarà l’output.
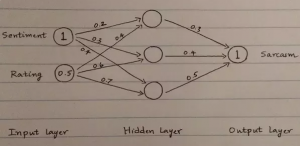
Ad ogni cerchio (o neurone) nel layer nascosto e di output, moltiplichiamo gli input con il peso corrispondente e sommiamo i risultati.

Hidden Layer 1 Neurone =(1∗0.2)+(0.5∗0.4)=0.4(1∗0.2)+(0.5∗0.4)=0.4
 
Hidden Layer 2 Neurone =(1∗0.3)+(0.5∗0.6)=0.6(1∗0.3)+(0.5∗0.6)=0.6
 
Hidden Layer 3 Neurone =(1∗0.4)+(0.5∗0.7)=0.75

Inoltre, vogliamo che l’output (Sarcasmo) sia un numero compreso tra 0 e 1 (altri valori non avrebbero senso). E questo lo facciamo usando una funzione magica sul layer di output che riduce ogni numero in un numero compreso tra 0 e 1.
Ogni funzione che applichiamo a livello di neurone è chiamata funzione d’attivazione e in questo caso, useremo la funzione sigmoid sul livello di output.

Final Layer = (0.4∗0.3)+(0.6∗0.4)+(0.75∗0.5)=0.735(0.4∗0.3)+(0.6∗0.4)+(0.75∗0.5)=0.735
 
Output = sigmoid(0.735)sigmoid(0.735) =0.324

Abbiamo dunque un output di 0.324. Ma ci aspettavamo 1! Quindi ora che facciamo? Cambiamo leggermente i pesi assegnati agli archi per portarci verso il valore corretto. Lo facciamo usando un metodo chiamato Back propagation, spiegata in questo blog.

Ripetiamo questo step migliaia di volte sui nostri dati di Training, regolando di volta in volta i nostri pesi. Con l’obiettivo di ottenere un peso ideale per predirre al meglio il Sarcasmo dato sentiment e rating.

Tutto qua, la maggior parte degli applicativi di Neural Network non sono altro che variazioni di quanto appena visto sopra. Con modifiche su:

– Struttura di input e output.
– Il numero di layer nascosti e neuroni.
– Le connessioni fra neuroni.
– Il processo di Training.
– Le funzioni di attivazione.

Commentate e condividete se vi è tornato utile!